Introduction
Cluster analysis is a way of “slicing and dicing” data to allow the
grouping together of similar entities and the separation of dissimilar
ones. Issues arise due to the existence of a diverse number of
clustering algorithms, each with different techniques and inputs, and
with no universally optimal methodology. Thus, a framework for cluster
analysis and validation methods are needed. Our approach is to use
cluster ensembles from a diverse set of algorithms. This ensures that
the data has been considered from several angles and using a variety of
methods. We have currently implemented about 15 clustering algorithms,
and we provide a simple framework to add additional algorithms (see
example("consensus_cluster")). Although results are
dependent on the subset of algorithms chosen for the ensemble, the
intent is that we capture a variety of clustering outputs and select
those that are most consistent with the data.
You can install diceR from CRAN with:
install.packages("diceR")Or get the latest development version from GitHub:
# install.packages("devtools")
devtools::install_github("AlineTalhouk/diceR")We load an excerpt of an expression data set from TCGA of 100 high grade serous carcinoma samples measured on 50 genes.
Clustering Algorithms
The list of clustering algorithms available for use are:
-
"nmf": Nonnegative Matrix Factorization (using Kullback-Leibler Divergence or Euclidean distance) -
"hc": Hierarchical Clustering -
"diana": DIvisive ANAlysis Clustering -
"km": K-Means Clustering -
"pam": Partition Around Medoids -
"ap": Affinity Propagation -
"sc": Spectral Clustering using Radial-Basis kernel function -
"gmm": Gaussian Mixture Model using Bayesian Information Criterion on EM algorithm -
"block": Biclustering using a latent block model -
"som": Self-Organizing Map (SOM) with Hierarchical Clustering -
"cmeans": Fuzzy C-Means Clustering -
"hdbscan": Hierarchical Density-based Spatial Clustering of Applications with Noise (HDBSCAN)
They are passed as a character vector into the
algorithms parameter of consensus_cluster().
Note that the list continues to evolve as we implement more algorithms
into diceR.
Cluster Models
The clustering algorithms can be categorized under different models or paradigms based on how the clusters are formed. We provide a brief overview to guide the initial selection of algorithms since no single algorithm works for every data model.1
- Connectivity Models:
"hc"and"diana"are hierarchical models based on connecting objects using a particular similarity or distance metric. - Centroid Models:
"km"and"pam"uses initial cluster centers calculated based on the mean of the objects, where"pam"restricts the centroid to be an actual object. These models are good for modeling data that produces spherical clusters."ap"is similar to"pam"because it calculates “exemplars” (like centroids) of the data but is advantageous because initialization of k (number of clusters) is not required.2"cmeans"is similar to"km"except that points can be assigned to more than one cluster. - Distribution Models:
"gmm"assumes a Gaussian mixture model used by the EM algorithm for clustering.3 The gain in model complexity is traded with utility since the assumption is quite strong. - Density Models:
"hdbscan"runs hierarchical clustering on the DBSCAN result.4,5 These models assume that each cluster has high density, so when there are overlapping regions, the algorithms may not be able to separate objects that well. - Subspace Models:
"block"clusters both samples and features, so is useful when you want to associate these pairs of cluster entities (e.g. are there functional gene groups that associate with sample subtypes?). Our implementation uses the latent block model.6 - Neural Models: our implementation of
"som"reduces the data to a two-dimensional subspace using a neural network model, before performing hierarchical clustering.7 A lot of the noise is phased out and cluster stability can be improved from using"hc"alone. - Spectral Clustering: Similar to
"som","sc"also performs dimensionality reduction before clustering, but instead uses eigenvectors of a kernel matrix.8 We use a radial-basis kernel function in the package. - Non-negative Matrix Factorization: the computational complexity with
"nmf"is doubled compared to other algorithms because data manipulations need to be performed to transform the input data into a non-negative matrix. Otherwise, NMF has a natural clustering result that can be used to group together samples and/or features.9
Distance Measures
The list of distance measures available for use are those found in
stats::dist and the spearman distance:
-
"euclidean": seestats::dist -
"maximum": seestats::dist -
"manhattan": seestats::dist -
"canberra": seestats::dist -
"binary": seestats::dist -
"minkowski": seestats::dist -
"spearman": based onbioDist::spearman.dist
They are passed as a character vector into the distance
parameter of consensus_cluster(). Only the
"hc", "diana", "pam" algorithms
use the distance parameter.
Validity Indices
Internal
The list of internal validity indices used for evaluating clusters are:
- Calinski-Harabasz, Dunn, PBM, Tau, Gamma, C-index, Davies-Bouldin,
McClain-Rao, SD, Ray-Turi, G-plus, Rousseeuw’s Silhouette, and S-Dbw
from the
clusterCriR package - Dunn index and Connectivity measure from the
clValidR package - Compactness measure from the
LinkCluEMATLAB package
External
The list of external validity indices used for evaluating clusters are:
- Hubert, Jaccard, McNemar, and Rand indices adapted from the archived
clusterCritR package - Normalized mutual information (NMI) calculated using
infotheo::entropy() - Overall confusion matrix statistics from
caret::confusionMatrix: “Overall Accuracy”, “Cohen’s kappa”, “No Information Rate”, “P-Value [Acc > NIR]” - Averaged class-specific confusion matrix statistics: “Sensitivity”, “Specificity”, “PPV”, “NPV”, “Detection Rate”, “Accuracy”, “Balanced Accuracy”
Consensus Clustering
When Monti et al. (2003) first introduced consensus clustering, the idea was to use one clustering algorithm on bootstrapped subsamples of the data. We implement some extensions where a consensus is reached across subsamples and across algorithms. The final cluster assignment is then computed using statistical transformations on the ensemble cluster.
The base function of this package is
consensus_cluster(), which outputs cluster assignments
across subsamples and algorithms, for different k (number of clusters).
For example, let’s say we were interested in clustering the
hgsc data into 3 or 4 clusters, using 80% resampling on 5
replicates, for these clustering algorithms: Hierarchical Clustering,
PAM, and DIvisive ANAlysis Clustering (DIANA). Euclidean distance is
used for all algorithms.
CC <- consensus_cluster(
hgsc,
nk = 3:4,
p.item = 0.8,
reps = 5,
algorithms = c("hc", "pam", "diana"),
progress = FALSE
)The output is a 4-dimensional array: rows are samples, columns are different bootstrap subsample replicates, slices are algorithms, and each “box” (4th dimension) is for a different k. Below are the first few cluster assignments for each replicate in the DIANA algorithm for k = 3.
co <- capture.output(str(CC))
strwrap(co, width = 80)
#> [1] "int [1:100, 1:5, 1:3, 1:2] 1 1 NA NA NA 1 1 NA 1 NA ..."
#> [2] "- attr(*, \"dimnames\")=List of 4"
#> [3] "..$ : chr [1:100] \"TCGA.04.1331_PRO.C5\" \"TCGA.04.1332_MES.C1\""
#> [4] "\"TCGA.04.1336_DIF.C4\" \"TCGA.04.1337_MES.C1\" ..."
#> [5] "..$ : chr [1:5] \"R1\" \"R2\" \"R3\" \"R4\" ..."
#> [6] "..$ : chr [1:3] \"HC_Euclidean\" \"PAM_Euclidean\" \"DIANA_Euclidean\""
#> [7] "..$ : chr [1:2] \"3\" \"4\""| R1 | R2 | R3 | R4 | R5 | |
|---|---|---|---|---|---|
| TCGA.04.1331_PRO.C5 | 2 | 2 | 1 | 1 | 1 |
| TCGA.04.1332_MES.C1 | 1 | 2 | 1 | 1 | 1 |
| TCGA.04.1336_DIF.C4 | NA | 1 | NA | 2 | NA |
| TCGA.04.1337_MES.C1 | NA | NA | 2 | 2 | 2 |
| TCGA.04.1338_MES.C1 | NA | NA | 2 | 2 | 2 |
| TCGA.04.1341_PRO.C5 | 2 | NA | 1 | NA | 1 |
Note the unavoidable presence of NAs because we used 80%
subsampling. This can be problematic in certain downstream ensemble
methods, so we can impute missing values using K-Nearest Neighbours
beforehand. There might still be NAs after KNN because of
how the decision threshold was set. The remaining missing values can be
imputed using majority voting.
CC <- apply(CC, 2:4, impute_knn, data = hgsc, seed = 1)
CC_imputed <- impute_missing(CC, hgsc, nk = 4)
sum(is.na(CC))
#> [1] 2
sum(is.na(CC_imputed))
#> [1] 0We can carry on the analysis using either CC or
CC_imputed.
Consensus Functions
diceR provides functions for retrieving useful summaries
and other results for consensus clustering.
Compute consensus matrix with consensus_matrix()
The consensus matrix is an n by n matrix, where n is the number of
samples. Each element is a real-valued number between 0 and 1 inclusive,
representing the proportion of times that two samples were clustered
together out of the times that the same samples were chosen in the
bootstrap resampling. The diagonal are all one’s. Suppose we wanted to
compute the consensus matrix for PAM, k = 4, and visualize using
graph_heatmap():
pam.4 <- CC[, , "PAM_Euclidean", "4", drop = FALSE]
cm <- consensus_matrix(pam.4)
dim(cm)
#> [1] 100 100
hm <- graph_heatmap(pam.4)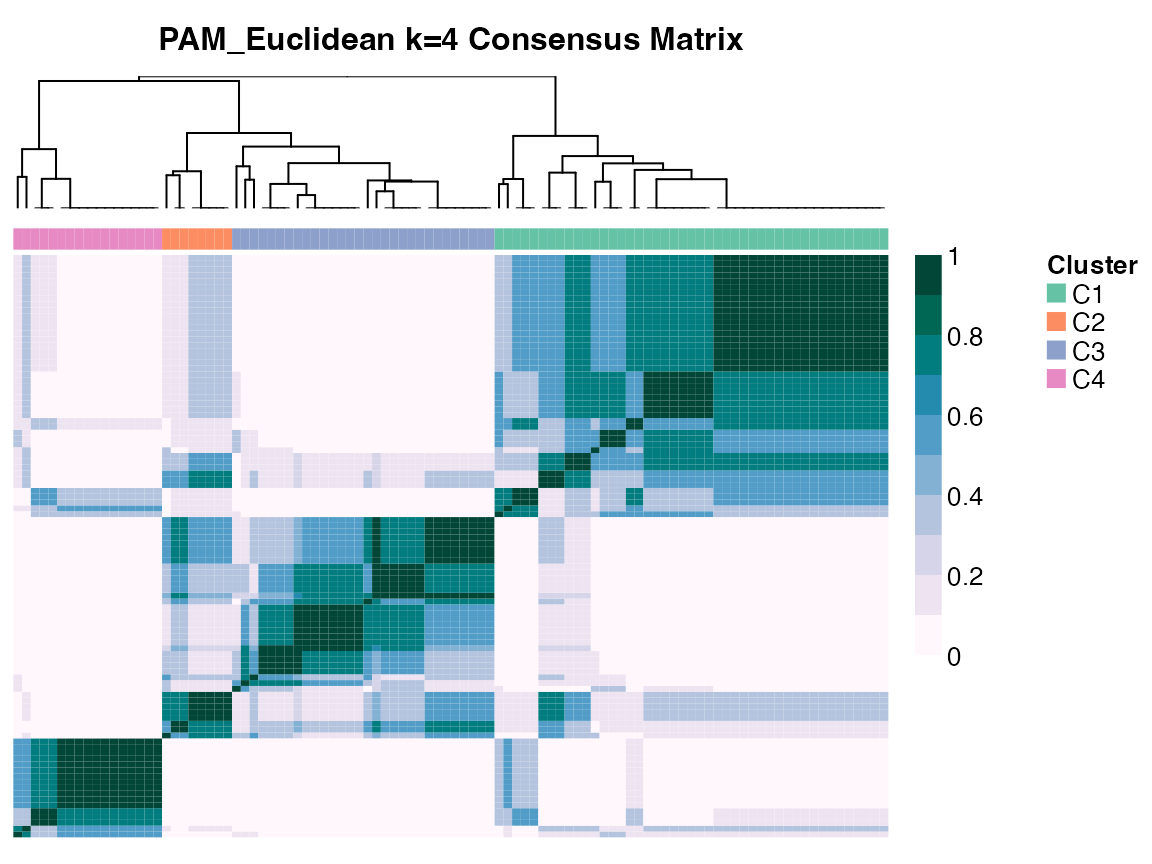
Consensus Matrix Heatmap
Combine consensus summaries with
consensus_combine()
If we wish to separately extract consensus matrices and consensus
classes for every algorithm, consensus_combine() is a
convenient wrapper to do so. Setting element = "matrix"
returns a list of consensus matrices. On the other hand, setting
element = "class" returns a matrix with rows as samples,
and columns as clustering assignments for each algorithm.
ccomb_matrix <- consensus_combine(CC, element = "matrix")
ccomb_class <- consensus_combine(CC, element = "class")
str(ccomb_matrix, max.level = 2)
#> List of 2
#> $ 3:List of 3
#> ..$ HC_Euclidean : num [1:100, 1:100] 1 0.8 1 0.8 1 1 1 1 1 1 ...
#> ..$ PAM_Euclidean : num [1:100, 1:100] 1 1 0.2 0.8 0 1 1 0.8 0 0.2 ...
#> ..$ DIANA_Euclidean: num [1:100, 1:100] 1 0.8 0 0 0 1 1 0 0 1 ...
#> $ 4:List of 3
#> ..$ HC_Euclidean : num [1:100, 1:100] 1 0.6 1 0.6 1 1 1 1 1 0.8 ...
#> ..$ PAM_Euclidean : num [1:100, 1:100] 1 1 0.2 0.8 0 0.8 0.8 0.6 0 0 ...
#> ..$ DIANA_Euclidean: num [1:100, 1:100] 1 0.8 0 0 0 1 1 0 0 1 ...| HC_Euclidean | PAM_Euclidean | DIANA_Euclidean |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1 | 1 |
| 1 | 2 | 2 |
| 2 | 1 | 2 |
| 1 | 3 | 2 |
| 1 | 1 | 1 |
One can feed in ccomb_class (instead of CC)
into consensus_matrix() to obtain a consensus matrix across
subsamples and algorithms (and k).
# consensus matrix across subsamples and algorithms within k = 3
cm_k3 <- consensus_matrix(ccomb_class$`3`)
# consensus matrix across subsamples and algorithms within k = 4
cm_k4 <- consensus_matrix(ccomb_class$`4`)
# consensus matrix across subsamples and algorithms and k
cm_all <- consensus_matrix(ccomb_class)A situation might also arise where we initially decided on using 3
clustering algorithms for the ensemble, but later wish to add additional
algorithms for analysis. consensus_combine() takes in any
number of ensemble objects (e.g. CC and CC2)
and combines the results.
CC2 <- consensus_cluster(
hgsc,
nk = 3:4,
p.item = 0.8,
reps = 5,
algorithms = "km",
progress = FALSE
)
ccomb_class2 <- consensus_combine(CC, CC2, element = "class")| HC_Euclidean | PAM_Euclidean | DIANA_Euclidean | KM |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 |
| 1 | 2 | 2 | 2 |
| 2 | 1 | 2 | 2 |
| 1 | 3 | 2 | 2 |
| 1 | 1 | 1 | 3 |
Evaluate, trim, and reweigh algorithms with
consensus_evaluate()
Internal cluster validation indices assess the performance of results
by taking into account the compactness and separability of the clusters.
We choose a variety of indices on which to compare the collection of
clustering algorithms. We use the PAC (Proportion of Ambiguous
Clusters), the proportion of entries in a consensus matrix that are
strictly between lower (defaults to 0) and
upper (defaults to 1), to give a measure of cluster
stability. In addition, if no reference class is provided, we calculate
the average PAC across algorithms within each k, and choose
the k with the greatest average PAC. If there is a
reference class, k is the number of distinct classes in the
reference.
ccomp <- consensus_evaluate(hgsc, CC, CC2, plot = FALSE)| Algorithms | calinski_harabasz | dunn | pbm | tau | gamma | |
|---|---|---|---|---|---|---|
| HC_Euclidean | HC_Euclidean | 4.24 | 0.4205 | 11.98 | -2.012e-05 | -2.088 |
| PAM_Euclidean | PAM_Euclidean | 15.4 | 0.2849 | 7.175 | 6.306e-06 | -1.186 |
| DIANA_Euclidean | DIANA_Euclidean | 12.47 | 0.28 | 6.425 | -6.407e-06 | 1.279 |
| KM | KM | 17.22 | 0.3162 | 6.495 | 5.471e-06 | 0.7544 |
| c_index | davies_bouldin | mcclain_rao | sd_dis | ray_turi | g_plus | |
|---|---|---|---|---|---|---|
| HC_Euclidean | 0.202 | 1.591 | 0.7303 | 0.3595 | 0.954 | 7.184e-06 |
| PAM_Euclidean | 0.1882 | 2.341 | 0.7881 | 0.6273 | 2.008 | 6.613e-06 |
| DIANA_Euclidean | 0.1871 | 1.969 | 0.7822 | 0.4838 | 1.654 | -9.96e-06 |
| KM | 0.1599 | 1.9 | 0.7685 | 0.4727 | 1.247 | 5.715e-07 |
| silhouette | s_dbw | Compactness | Connectivity | |
|---|---|---|---|---|
| HC_Euclidean | 0.1171 | NA | 7.833 | 19.03 |
| PAM_Euclidean | 0.08106 | NA | 6.831 | 65.74 |
| DIANA_Euclidean | 0.02616 | NA | 7.081 | 47.95 |
| KM | 0.112 | NA | 6.704 | 62.96 |
We see that the biclustering algorithm is the least ambiguous and also most well-clustered (high compactness and separability).
Some algorithms perform too poorly to deserve membership in the cluster ensemble. We consider the relative ranks of each algorithm across all internal indices, and compute their sum. All algorithms below a certain quantile for the sum rank are trimmed (removed). By default this quantile is 75%.
After trimming, we can optionally choose to reweigh the algorithms based on the internal index magnitudes. Of course, we take into account the direction of optimality (higher is better is lower is better). Algorithms reweighed are then fed into the consensus functions. This is done by replicating each algorithm by a scalar factor that is proportional to its weight. For example, if we have two algorithms A and B, and A is given a weight of 80% and B is given a weight of 20%, then we make 4 copies of A and 1 copy of B. To minimize computational time, the total number of copies out of all algorithms has an upper bound of 100. Without reweighing, each algorithm is given equal weight.
ctrim <- consensus_evaluate(hgsc, CC, CC2, trim = TRUE, reweigh = FALSE, n = 2)
str(ctrim, max.level = 2)
#> List of 5
#> $ k : int 4
#> $ pac :'data.frame': 2 obs. of 5 variables:
#> ..$ k : chr [1:2] "3" "4"
#> ..$ HC_Euclidean : num [1:2] 0.134 0.397
#> ..$ PAM_Euclidean : num [1:2] 0.458 0.451
#> ..$ DIANA_Euclidean: num [1:2] 0.248 0.233
#> ..$ KM : num [1:2] 0.282 0.272
#> $ ii :List of 2
#> ..$ 3:'data.frame': 4 obs. of 16 variables:
#> ..$ 4:'data.frame': 4 obs. of 16 variables:
#> $ ei : NULL
#> $ trim.obj:List of 5
#> ..$ alg.keep : chr [1:2] "HC_Euclidean" "KM"
#> ..$ alg.remove : chr [1:2] "PAM_Euclidean" "DIANA_Euclidean"
#> ..$ rank.matrix:List of 1
#> ..$ top.list :List of 1
#> ..$ E.new :List of 1The return value shows which algorithms were kept, removed (if any), and the trimmed (and potentially reweighed) cluster ensemble.
Significance Testing
To test whether there are four statistically distinct clusters (k =
4) versus no clusters (k = 1) using the PAM algorithm, we run
sigclust with 50 simulations and generate a p-value for
this significance test.
set.seed(1)
pam_4 <- ccomb_class2$`4`[, "PAM_Euclidean"]
sig_obj <- sigclust(hgsc, k = 4, nsim = 100, labflag = 0, label = pam_4)
co <- capture.output(str(sig_obj))
strwrap(co, width = 80)
#> [1] "Formal class 'sigclust' [package \"sigclust\"] with 10 slots"
#> [2] "..@ raw.data : num [1:100, 1:50] -0.0107 -0.7107 0.8815 -1.0851 -0.9322 ..."
#> [3] ".. ..- attr(*, \"dimnames\")=List of 2"
#> [4] ".. .. ..$ : chr [1:100] \"TCGA.04.1331_PRO.C5\" \"TCGA.04.1332_MES.C1\""
#> [5] "\"TCGA.04.1336_DIF.C4\" \"TCGA.04.1337_MES.C1\" ..."
#> [6] ".. .. ..$ : chr [1:50] \"ABAT\" \"ABHD2\" \"ACTB\" \"ACTR2\" ..."
#> [7] "..@ veigval : num [1:50] 11.81 4.51 2.66 2.29 1.84 ..."
#> [8] "..@ vsimeigval: num [1:50] 11.81 4.51 2.66 2.29 1.84 ..."
#> [9] "..@ simbackvar: num 0.42"
#> [10] "..@ icovest : num 2"
#> [11] "..@ nsim : num 100"
#> [12] "..@ simcindex : num [1:100] 0.624 0.692 0.664 0.672 0.637 ..."
#> [13] "..@ pval : num 0.23"
#> [14] "..@ pvalnorm : num 0.206"
#> [15] "..@ xcindex : num 0.63"The p-value is 0.23, indicating we do not have sufficient evidence to
conclude there are four distinct clusters. Note that we did not use the
full hgsc data set in this example, so the underlying
biological mechanisms may not be fully captured.
References
- Estivill-Castro, Vladimir (20 June 2002). “Why so many clustering algorithms — A Position Paper”. ACM SIGKDD Explorations Newsletter. 4 (1): 65–75.
- Brendan J. Frey; Delbert Dueck (2007). “Clustering by passing messages between data points”. Science. 315 (5814): 972–976.
- C. Fraley, A. E. Raftery, T. B. Murphy and L. Scrucca (2012). mclust Version 4 for R: Normal Mixture Modeling for Model-Based Clustering, Classification, and Density Estimation. Technical Report No. 597, Department of Statistics, University of Washington.
- Campello, R. J. G. B.; Moulavi, D.; Sander, J. (2013). Density-Based Clustering Based on Hierarchical Density Estimates. Proceedings of the 17th Pacific-Asia Conference on Knowledge Discovery in Databases, PAKDD 2013, Lecture Notes in Computer Science 7819, p. 160.
- Campello, Ricardo JGB, et al. “Hierarchical density estimates for data clustering, visualization, and outlier detection.” ACM Transactions on Knowledge Discovery from Data (TKDD) 10.1 (2015): 5.
- G. Govaert and M. Nadif. Latent block model for contingency table. Communications in Statistics - Theory and Methods, 39(3):416–425, 2010.
- Isa, Dino, V. P. Kallimani, and Lam Hong Lee. “Using the self organizing map for clustering of text documents.” Expert Systems with Applications 36.5 (2009): 9584-9591.
- Andrew Y. Ng, Michael I. Jordan, Yair Weiss On Spectral Clustering: Analysis and an Algorithm Neural Information Processing Symposium 2001
- Brunet J, Tamayo P, Golub TR and Mesirov JP (2004). “Metagenes and molecular pattern discovery using matrix factorization.” Proceedings of the National Academy of Sciences of the United States of America, 101(12), pp. 4164-9.
